一分鐘準備段考
- 清楚每個物理名詞的定義
- 公式不要死記,要能推導
- 利用名師學院系列產品,反覆觀看、補強弱點
|
萬有引力
一、古代天體運行理論與克卜勒定律產生的背景
1. 地球中心說:希臘哲學家托勒密結合宗教、傳說與簡單觀測的結果,推論地球為宇宙的中心,日、月與其他行星皆繞地球運轉。
2. 太陽中心說:波蘭天文學家哥白尼提出太陽才是宇宙中心的觀點,地球與其他各行星皆繞太陽運轉。
3. 丹麥天文學家第谷.布拉依據其觀測結果,認為地球為宇宙的中心,太陽繞地球運轉,而其他行星則是繞太陽運行。
4. 德國天文學家克卜勒依據其老師第谷.布拉大量的觀測結果,分析歸納出行星運動的三大定律,並推翻以地球為宇宙中心的論點,提出太陽才是宇宙中心的看法。
5. 至今科學界了解太陽亦非宇宙的中心,且了解到宇宙中存在許多不同結構與不同尺度大小的天體,太陽只是眾多恆星中的其中一顆恆星而已,但克卜勒所提出的行星運動三大定律,為天體運行的研究帶來了重大的突破。
二、克卜勒第一定律(軌道定律,1609 年)
1. 定律內容:行星繞太陽運行,在以太陽為兩焦點之一的橢圓軌道上運行。
三、克卜勒第二定律(等面積定律,1609 年)
1. 定律內容:行星繞太陽運行,其與太陽間的連線,在相同的時間內掠掃過相等的面積。
2. 面積速率公式: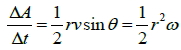 =定值 =定值
(隨各行星而異) |
|
3. 若行星位於橢圓軌道長軸的兩
端點(即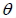 = 90°),則可得: = 90°),則可得: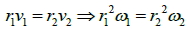 |
|
四、克卜勒第三定律(週期定律,1619 年)
1. 定律內容:各行星繞太陽運行,其與太陽間平均距離的立方,與其週期平方的比值均相同,而與行星無關。
2. 公式: 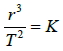 ,其中  五、克卜勒行星運動定律的探討
1. 克卜勒第二定律適用於探討同一行星,在同一橢圓軌道上運行時,不同時刻與不同位置狀況的分析。 2. 克卜勒第三定律適用於探討不同行星繞同一恆星,或是不同衛星繞同一行星的狀況。 3. 若假設行星作等速率圓周運動,則面積速率 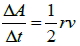 ,週期 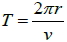 六、萬有引力定律
1. 定律內容:兩質點間萬有引力的量值,與兩質點的質量乘積成正比,而與兩質點間的距離平方成反比。
2. 公式: 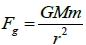 ,其中 G 稱為 萬有引力常數(重力常數),由卡文狄西
首先以扭秤實驗測得,近年精準的測定值為 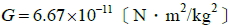 3. 萬有引力方向:在兩質點的連心線上,為一對作用力與反作用力。
七、由克卜勒定律推導出萬有引力定律
1. 首先考慮月球繞地球作圓周運動時,需要向心力,假設月球質量為 m ,則向心力: 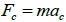 2. 由等速率圓周運動的向心力結合克卜勒第三定律:
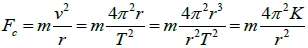 3. 假設地球質量為 M ,令 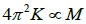 ,由牛頓第三運動定律:
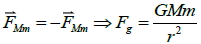 八、重力加速度(重力場)
1. 定義:重力加速度是指物體僅受重力作用時所產生的加速度,通常以 g 為代表符號。
2. 質量為 m 的物體與質量為 M 的地球中心距離為 r 時( r 大於地球半徑),
所受到的重力 mg 即等於其與地球之間的萬有引力 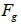 ,即 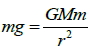 ,,所
以重力加速度 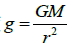 ;此為地球外的重力加速度量值,加速度方向指向地心。 九、衛星運動(以圓形軌道計算)
1. 力:衛星所受萬有引力提供其作圓周運動所需的向心力,即 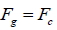
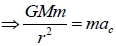 2. 向心加速度: 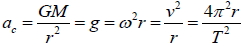 3. 速率: 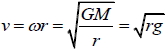 4. 週期: 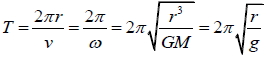 5. 克卜勒第三定律: 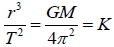 十、地表衛星
1. 地表衛星的軌道半徑 r 約等於地球的半徑 R 。
2. 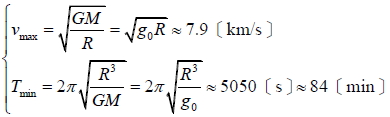 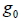 :專指地球本身於地表產生的重力加速度。 十一、同步衛星
1. 同步衛星的繞行週期 T 約等於地球的自轉週期。
2.  十二、人造衛星繞行星公轉時,其內部的物體是處於失重的狀態。
十三、地球自轉對物體視重的影響
1. 物體在赤道上:
離心力 =  2. 物體在南北極上:
離心力 = 0,視重 = 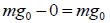

|




