一分鐘準備段考
- 基本定義和題型要「熟」,不是只要「會」
- 解出一題難題勝過解十題簡單的題目,不要逃避不會的題目
- 多做題目,培養對題型的解題感覺
- 利用名師學院系列產品,反覆觀看、補強弱點
|
拋物線
一、拋物線的定義
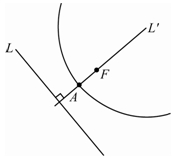
設 L 為一定直線, F 為不在 L 上的一定點, 則在包含 L 與 F 的平面上, 至 F 與 L 等距離的所有點所成的圖形, 稱為拋物線。
其中, L 稱為拋物線的準線;F 稱為拋物線的焦點;過焦點 F 且與準線 L 垂直的直線 L' 稱為拋物線的對稱軸
(簡稱為軸);對稱軸 L' 與拋物線的交點 A 稱為拋物線的頂點。 |
|
二、拋物線的標準式
三、拋物線的動點參數式假設法
橢圓
一、橢圓的定義
1. 坐標平面上, 二定點 F、F' , 若 P 點至二定點的距離和為定值(設該定值為 2a, 且 a > 0), 即
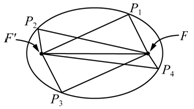
, 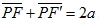 則這樣的 P 點所成的圖形稱為橢圓, 其中 F 與 F' 稱為橢圓的二焦點。 則這樣的 P 點所成的圖形稱為橢圓, 其中 F 與 F' 稱為橢圓的二焦點。 |
|
2.
限制條件: 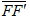 < 2 a二、橢圓的標準式
橢圓的標準式:設 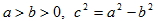
雙曲線
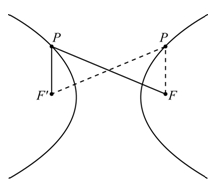
一、雙曲線的定義
1. 坐標平面上, 二定點 F、 F' , 若 P 點至二定點的距離差為定值(設該定值為 2a, 且 a > 0), 即 ,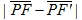 = 2a 則這樣的 P 點所成圖形稱為雙曲線, 其中 F 與 F' 稱為雙曲線的二焦點。 = 2a 則這樣的 P 點所成圖形稱為雙曲線, 其中 F 與 F' 稱為雙曲線的二焦點。
2. 限制條件: 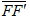 > 2a > 2a |
 |
二、雙曲線的標準式
雙曲線的標準式:設 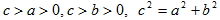
三、雙曲線的漸近線
1. 若雙曲線 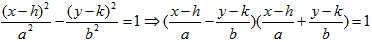 ,則雙曲線的二漸近線為 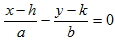 與 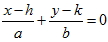 ,又可化為 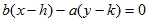 與 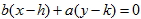 。 2. 若已知雙曲線的二條漸近線方程式為 L1: 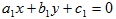 與 L2: 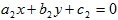 ,則可假設此雙曲線的方程式為 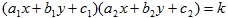 。

|
|