一分鐘準備段考
- 基本定義和題型要「熟」,不是只要「會」
- 解出一題難題勝過解十題簡單的題目,不要逃避不會的題目
- 多做題目,培養對題型的解題感覺
- 利用名師學院系列產品,反覆觀看、補強弱點
|
矩陣
一、矩陣的定義
1. 將一些數排列成矩形的陣列, 稱為「矩陣」。
2. 矩陣中同一水平線的各元稱為「列」;矩陣中同一鉛直線的各元稱為「行」。
3. 一個有 m 列、n 行的矩陣, 稱為「m × n 階矩陣」;若 m = n , 則又稱為「方陣」。
4. 「 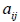 」代表矩陣中第 i 列, 第 j 行的元。 5. 將方程組的各項未知數係數列出排成的矩陣, 稱為「係數矩陣」。
6. 將方程組的「係數矩陣」再增設一行常數後, 稱為「增廣矩陣」。
二、矩陣的列運算
1. 將矩陣某列的每一元同乘以一個不為零的數。
2. 將矩陣某列的每一元同乘以不為零的數後, 再加至另一列的對應元。
3. 將矩陣的某兩列互換位置。
三、轉置矩陣
設矩陣 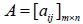 , 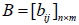 ,若 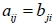 , 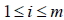 , 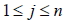 ,則稱 B 為 A 的轉置矩陣,以 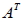 表之,即 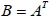 。 四、矩陣加法的性質
1. A + B = B + A (交換律)
2. (A + B) + C = A + (B + C) (結合律)
3. A + O = O + A = A (加法單位元素)
4. A + (−A) = O (加法反元素)
五、矩陣係數積的性質
1. (−1) A = − A
2. 0 ‧ A = O
3. α (A + B) = αA +αB
4. (α + β )A = αA + βA
5. α (βA) = (αβ)A
六、轉置矩陣的性質
1. 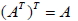 2. 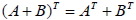 3. 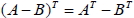 七、對稱矩陣
當矩陣 A 符合 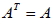 與 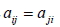 (對於所有的 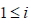 , 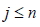 ), 則稱矩陣 A 為對稱矩陣。 八、反對稱矩陣
當矩陣 A 符合 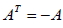 與 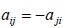 (對於所有的 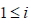 , 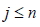 ), 則稱矩陣 A 為反對稱矩陣。 九、對稱矩陣與反對稱矩陣的異同
1. 皆為方陣。
2. 對稱矩陣的主對角線各元無限制;而反對稱矩陣的主對角線各元必為 0 。
十、單位矩陣的性質
1. 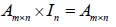 2. 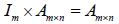 3. 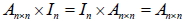 十一、矩陣的乘法性質
1. AB ≠ BA
2. A(BC) = (AB)C = ABC
3. A(B + C) = AB + AC
4. (A + B)C = AC + BC
5. 若 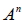 存在,則 A 為方陣 6. ( A + B)  = A + AB + BA+ B 7. ( I + B)  = I + IB + BI + B = I + 2B + B 8. ( A + B)  無二項式定理 9. 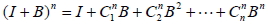 10. (rA)B = r(AB) , (rA)(sB) = (rs)(AB)
十二、二項式定理的應用
A、 B 皆為 n 階方陣, I 為 n 階單位方陣 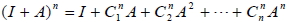
十三、若A 為一個轉移矩陣
若 A 為一個轉移矩陣, 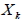 為由 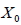 開始的第 k 次機率矩陣, 則: 1. A 中每一個元素為非負。
2. A 中每一行元素和為1。
3. 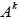 亦為轉移矩陣。 4. 若 k 趨於無限大, 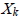 會趨於一個穩定態 X , 則 AX = X 。 十四、反方陣與可逆方陣
1. 設矩陣 A 為 n 階方陣, 若矩陣 B 滿足 AB = BA = 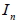 , 則稱 B 為 A 的乘法反元素或反方陣, 記為 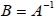 。 2. 具有反方陣的矩陣稱為可逆方陣。
十五、可逆方陣的性質與公式
設 A 、 B、 C 皆為可逆方陣且 A = ![A=[a b c d]](images/senior2-2-math-101-second-33.jpg) ,則: 1. A 的反方陣必唯一。
2. A 的行列式 det(A) ≠ 0
3. 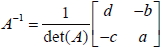 4. 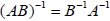 5. 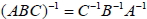 6. 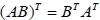 7. 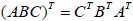 十六、方陣與聯立方程組
設 A = ![A=[a b c d]](images/senior2-2-math-101-second-33.jpg) 為可逆方陣, 則聯立方程組
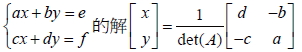 十七、矩陣與平移變換
1. 將坐標平面上的點 P , 沿 x 軸平移 h , 沿 y 軸平移 k,得新的坐標為 P' (x', y') ,則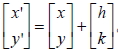 。 。
2. 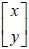 亦稱為行坐標。 亦稱為行坐標。
|
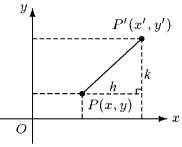 |
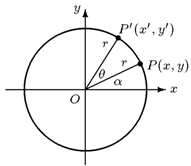
十八、矩陣與旋轉變換
1. 將坐標平面上的點 P (x, y) , 繞原點逆時針旋轉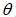 ,得新的點坐標為 P' (x',y' ) ,則 ,得新的點坐標為 P' (x',y' ) ,則
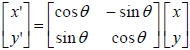 。 。
2. 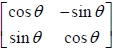 為旋轉矩陣。 為旋轉矩陣。 |
 |
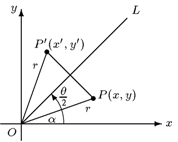
十九、矩陣與鏡射變換
1. 將坐標平面上的點 P (x, y) , 對 L(通過原點且斜角為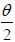 ) 鏡射後, 得新的坐標為 P' (x', y') , 則 ) 鏡射後, 得新的坐標為 P' (x', y') , 則
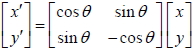 。 。
2. 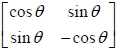 為鏡射矩陣。 為鏡射矩陣。 |
 |
二十、矩陣與伸縮變換
將坐標平面上的點 P ( x, y) , 以原點為中心, 伸縮 k 倍 ( k > 0) , 得新坐標為
P' ( x', y') ,則 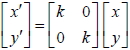 。 二十一、矩陣與推移變換
1. 將坐標平面上的點 P ( x, y) , 沿 x 軸推移 y 坐標的 k 倍, 得新坐標為 P' ( x', y'), 則
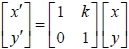 1. 將坐標平面上的點 P ( x, y) , 沿 y 軸推移 x 坐標的 k 倍, 得新坐標為 P' ( x', y'), 則
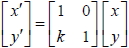 二十二、平面變換的性質
1. 有五種平移、旋轉、鏡射、伸縮與推移五種。
2. 其中以原點為中心的旋轉、伸縮、推移與過原點的直線為鏡射軸的鏡射均屬線性變換。
3. 平移、旋轉、鏡射等變換又稱為剛體變換, 其特性為形狀、大小、角度與面積均不改變。

|




