一分鐘準備段考
- 基本定義和題型要「熟」,不是只要「會」
- 解出一題難題勝過解十題簡單的題目,不要逃避不會的題目
- 多做題目,培養對題型的解題感覺
- 利用名師學院系列產品,反覆觀看、補強弱點
|
空間向量
1. 空間中兩直線 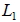 、 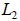 的關係有三種:
- 在同一平面上且二直線平行
- 在同一平面上且二直線相交
- 不在同一平面, 即兩直線歪斜
2. 空間中決定一個平面的條件:
- 不共線的三點
- 一直線與其線外一點
- 相交的兩直線
- 兩平行直線
3. 空間中一直線與平面的關係:
- 直線與平面平行(沒有交點)
- 直線與平面交於一點(一個交點)
- 直線與平面重合(無限多個交點)
4. 若空間中直線 L 與平面 E 互相垂直, 則:
- 過平面 E 上一定點 P 且垂直L的直線有無限多條。
- 所有這些直線構成平面 E 。
5. 設 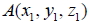 、 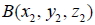 為空間坐標系中的二點, 則:
8. 空間中二向量 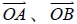 所張成的
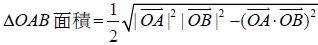 10. 柯西不等式:
設 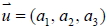 , 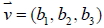 為空間中的兩向量, 則:
14. 三元一次聯立方程組 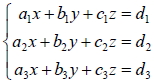 的 x、 y、 z 滿足 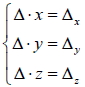 ,其中 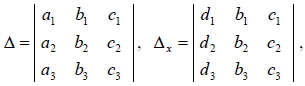
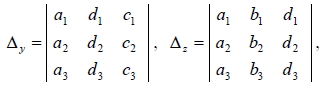 且:
- 當
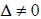 = 0 時,( x,y,z ) 恰有一組解 = 0 時,( x,y,z ) 恰有一組解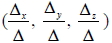 。 。
- 當
 = 0且 = 0且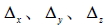 有一不為 0 時,無解。 有一不為 0 時,無解。
- 當
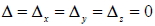 時, 可能無解, 也可能無限多解。 時, 可能無解, 也可能無限多解。
空間中的平面與直線
2. 平面 E 通過三點 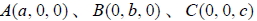 其中 a、 b、 c皆不為 0 , 則:
- 平面 E 之 x 軸的截距為 a , y 軸的截距為 b , z 軸的截距為 c 。
- 平面 E 的方程式可表為
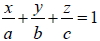 ,其法向量為 ,其法向量為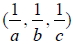
3. 空間中, 點 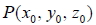 到平面 E : ax + by + cz + d = 0的距離
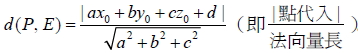 5. 空間中, 直線 L 通過定點 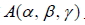 且與向量 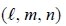 平行, 則: 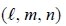 稱為直線的方向向量。 稱為直線的方向向量。- L 可表為
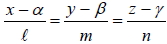 ,稱為直線L的對稱比例式, 簡稱比例式。 ,稱為直線L的對稱比例式, 簡稱比例式。
- L 可表為
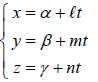 (其中 (其中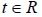 ), 稱為直線L的參數式。 ), 稱為直線L的參數式。
6. 直線 L 的二面式:
空間中, 直線 L 若為二平面 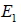 與 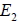 的交線, 則 L 可表為這兩個平面的聯立方程式, 此聯立方程式稱為直線 L 的二面式。
如:空間中, x 軸的二面式為 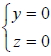 7. 設空間中二直線 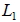 、 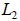 的方向向量分別為 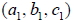 、 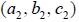 , 若不存在實數 k 使得 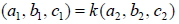 , 即,  、 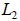 不平行, 則 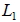 與 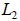 必相交或歪斜。 8. 空間中一直線與平面的關係: -
平行(沒有交點)。
- 交於一點(一個交點)。
- 重合(無限多個交點)。
9. 設直線 L 的方向向量為 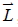 , 平面 E 的法向量為 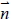 :
- 若
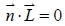 , 即
, 即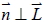 , 則 L 與 E 平行或重合。 , 則 L 與 E 平行或重合。
- 若
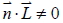 , 即 , 即 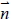 與 與 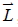 互不垂直, 則 L 與 E 相交(交於一點)。 互不垂直, 則 L 與 E 相交(交於一點)。
10. 設 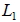 的方向向量為 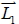
, 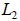 的方向向量為 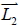
。若 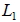 與 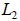 相交且交角為 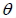 ,則 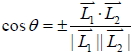 11. 設 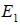 的法向量為 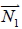
, 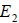 的法向量為 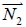 。若 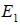 與 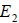 相交且交角為 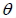 , 則
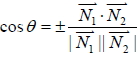 12. 設 L 的方向向量為 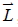
, E 的法向量為 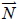 。若 L 與 E 相交且交角為 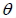 ,則
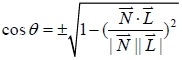
13. 空間中有一點 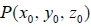 與一平面 E : ax + by + cz + d = 0 , 則: 投影點 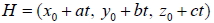
對稱點 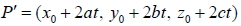
其中 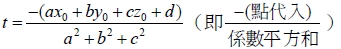
14. 過二平面 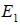 、 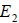 交線之所有平面 E 可設為 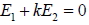 , 其中 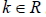 。
- 當 k = 0時, 則 E =
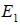 。 。
- 當 k 不存在時, 則 E =
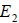 。 。

|
|




