一分鐘準備段考
- 基本定義和題型要「熟」,不是只要「會」
- 解出一題難題勝過解十題簡單的題目,不要逃避不會的題目
- 多做題目,培養對題型的解題感覺
- 利用名師學院系列產品,反覆觀看、補強弱點
|
機率
一、機率的基本概念
1. 樣本空間:一項試驗中所有可能發生的結果所成的集合, 常以代號 S 表示。
2. 樣本點:樣本空間的每一元素皆稱為樣本點。
3. 事件:樣本空間的每一個子集皆稱為一個事件, 而只含一個樣本點的事件稱為基本事件。
二、拉普拉斯之古典機率定義
S 為某試驗的樣本空間, 假設其中各基本事件發生的機會均等, 則對任一事件 A, 其發生機率為 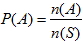 。
三、事件之間的關係
1. 和事件: A 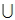 B B 表示由事件 A 和事件 B 的所有樣本所構成的事件。 2. 積事件: A 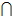 B B 表示由事件 A 和事件 B 共有的樣本所構成的事件。 3. 餘事件: 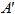 表示不在 A 中的樣本所構成的事件。 4. 互斥事件: A 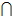 B = B = 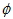 表示事件 A 和事件 B 不可能同時發生。 四、集合的運算公式
1. 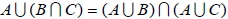 2. 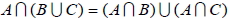 3. 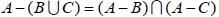 4. 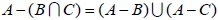 5. 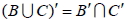 6. 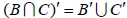 五、機率的性質與運算法則
1. 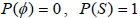 。 2. 若 A 和 B 為 S 中的二事件, 且 A 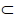 B,則 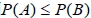 。 3. 若 A  S S 為一事件, 則 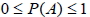 。 4. 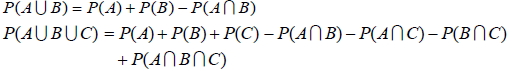 5. 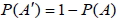 6. 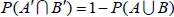 7. 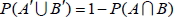 六、條件機率
在事件 B 發生的條件下, 事件 A 發生的機率, 稱為條件機率, 以 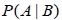 來表示,
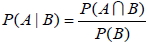 。 七、貝氏定理
設 A1、 A2、 A3、…、 An為樣本空間 S 的一個分割,其中 P ( Ai) > 0 , i = 1、2、...、 n,若  且 P( B) > 0,則:
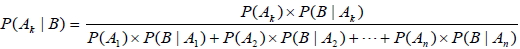 八、獨立事件的性質
若 P(A) > 0、P(B) > 0, 則下列三個式子必同時發生(一者成立, 另二者必成立)。
1. 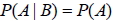 2. 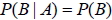 3. 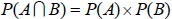 數據分析
一、平均數
1. 算術平均數:若有 n 個資料, 其值分別為 x1、 x2、...、 xn , 則此 n 個資料的算術平均數定義為 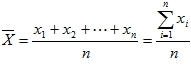 。 2. 加權平均數:一組資料 x1、 x2、...、 xn 中, 若所占的權數分別為 w1、 w2、...、 wn , 則此組資料的加權平均數為 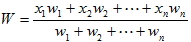 。 3. 幾何平均數: x1、 x2、...、 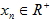 ,則此 n 個資料的幾何平均數 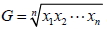 。 4. 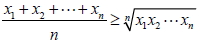 (算術平均數 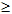 幾何平均數) 二、中位數(Me)
1. 將 n 個未分組資料, 依其大小順序由小而大排成一列。
- 若 n 為奇數, 則 Me 即為最中間項。
- 若 n 為偶數, 則 Me 為最中間二項的算術平均數。
2. n 個資料若已分組, 則中位數即第 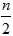 個。 三、全距(R)
1. 未分組資料︰全距 = 最大數 - 最小數
2. 已分組資料︰全距 = 最大上限 - 最小上限
四、四分位差
將一群統計資料由小而大排成一列, 則中位數 (Me)前段數值之中位數稱為第一四分位數 (Q1), 中位數 (Me) 後段數值之中位數稱為第三四分位數 (Q3), 而中位數 Me 可視為 Q2 (Me = Q2), 則規定四分位差 = Q3 - Q1
五、母體標準差
1. 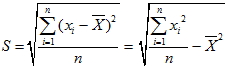 2. 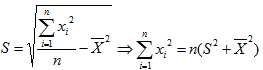 六、變異係數
在一般的情形下, 要比較兩組或兩組以上的資料的差異, 不能只比較標準差的大小, 需要一種相對的測度值作為比較的標準。
變異係數 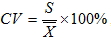 , 就是一種相對測度值, 其中 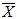 為算術平均數, S 為標準差。
變異係數較大, 表示這組資料的差異較大, 則這組資料的平均數 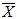 較不能反映集中趨勢。 七、相關係數
1. 各種變數(可量化的現象)之間的相互關係, 統計學上稱為相關性。
2. 兩種變量間的關係可用直線圖形適當表示者, 稱為直線相關。
3. 兩種變量間的關係可作曲線圖形適當表示者, 稱為曲線相關或非直線相關。
4. 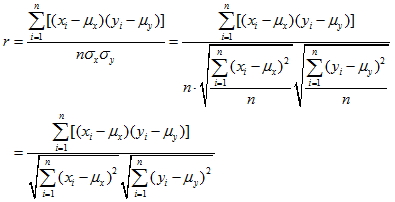

|




