一分鐘準備段考
- 基本定義和題型要「熟」,不是只要「會」
- 解出一題難題勝過解十題簡單的題目,不要逃避不會的題目
- 多做題目,培養對題型的解題感覺
- 利用名師學院系列產品,反覆觀看、補強弱點
|
排列、組合
一、敘述
為有絕對標準且可以判斷真假的句子。
二、符號
1. 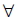 :所有的, 每一個, 任意的。 2. 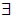 :存在, 有, 至少有一個。 3. ∧(且):一個敘述「p ∧ q」只有在 p、q 都是真的, 這個敘述才是真的。
4. ∨(或):一個敘述「p ∨ q」只要 p、q 其中一個是真的, 這個敘述就是真的。
三、狄莫根律
1. ~ ( p ∧ q) ≡ ~ p ∨ ~ q
2. ~ ( p ∨ q) ≡ ~ p ∧ ~ q
四、三一律
若 a、b ∈ R , 則:
1. ~ ( a = b ) ≡ a ≠ b ≡ a > b ∨ a < b
2. ~ ( a > b ) ≡ a ≤ b
3. ~ ( a < b ) ≡ a ≥ b
4. ~ ( a ≥ b ) ≡ a < b
5. ~ ( a ≤ b ) ≡ a > b
五、集合、元素的關係
1. A = { a, b, c}
- a 是集合 A 的元素, 稱 a 屬於 A , 記為 a ∈ A。
- a 不是集合 A 的元素, 稱 a 不屬於 A, 記為 a
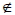 A。 A。
2. B ⊂ A:集合 B 為 A 的子集或部分集合。
3. 規定 φ 是任何集合之子集, 即 φ ⊂ A。
六、交集
A ∩ B = { x | x ∈ A 且 x ∈ B}
七、聯集
A ∪ B = { x | x ∈ A 或 x ∈ B}
八、差集
A − B = { x | x ∈ A 且 x 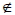 B B}
九、補集
設 U 表宇集, 則 A 的補集 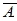 = { x | x ∈ U 且 x 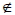 A A} 十、乘法原理
1. 若完成 E 事件的方法有 m 種, 完成 F 事件的方法有 n 種, 且 E、F 二事件互不影響, 則連續完成 E、F 兩事件的方法數為
(完成 E 的方法數) × (完成 F 的方法數) = m × n 。
十一、加法原理
若完成某件事情的方式有 E 、F 兩種, 其中 E 方式有 m 種方法完成, F 方式有 n 種方法完成, 且 E 、F 兩方式不能同時發生, 則完成此件事情的所有方法數為
(完成 E 的方法數) + (完成 F 的方法數) = m + n 。
十二、直線排列
有 n 個不同物件, 若從中任意取 r 個作直線排列, 但不重複選取, 則所有可能的結果總數, 稱為 n 中取 r 的排列數, 以 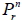 表示。
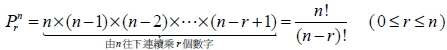 十三、重複排列
由 n 種不同的物件中, 任選出 r 個排成一列, 且可以重複選取, 則稱為 n 中取 r 的重複排列, 重複排列數以 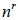 表示。 十四、不盡相異物的排列
設有 n 個物件, 共有 k 種不同的種類, 第 1 類有 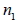 個, 第 2 類有
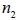 個, …, 第 k 類有 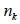 個(其中 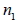 + 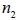 +‧‧‧+ 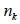 = n ), 將此 n 個物件排成一列的方法數為
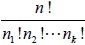 。 十五、組合
在不論取出物件的先後順序情況下, 從 n 個不同的物件中任取 r 個為一組, 但不重複選取, 則所有可能的結果總數, 稱為 n 中取 r 的組合數, 以 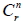 或 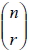 表示。 1. 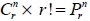 2. 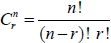 3. 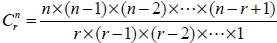 4. 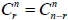 十六、排容原理
設 A、B、C 為有限集合, 若 A、B、C 中所含的元素個數以 n(A)、n(B)、n(C)表示, 則:
1. n(A ∪ B) = n(A) + n(B) − n(A ∩ B)
2. n(A ∪ B ∪C) = n(A) + n(B) + n(C) − n(A ∩ B) − n(A ∩ C) − n(B ∩C) + n(A ∩ B ∩C)
十七、路徑的計數問題
若棋盤式方格為 m× n 格, 則由一端走捷徑至對角線的另一端之路線總數為 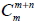 十八、相異直線決定交點
1. 平面上設有 n 條相異直線, 若其中任三條直線均不共點, 則可決定 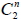 個交點。 2. 平面上設有 n 條相異直線, 若其中 m 條直線恰交於一點, 且其餘任三條直線均不共點, 則可決定 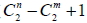 個交點。 十九、棋盤方格
若棋盤的橫線有 n 條、縱線有 m 條, 則共可決定 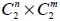 個矩形。 二十、重複組合
1. 若 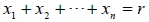 (其中 n ∈ N 且 r ≥ 0), 則 ( 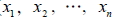 ) 的非負整數解共有 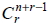 組。 2. n 種不同物, 組成 r 個的方法數用 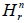 表示。 3. 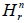 恰為 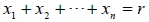 的非負整數解組數。 4. 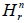 = 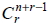 二十一、二項式定理
二十二、多項式展開
二十三、巴斯卡定理

|




