一分鐘準備段考
- 清楚每個物理名詞的定義
- 公式不要死記,要能推導
- 整理比較,如摩擦力的特徵、牛頓運動定律等
- 利用名師學院系列產品,反覆觀看、補強弱點
|
靜力學概論
一、「力」的要素與單位
1. 力的三要素為大小(量值)、方向、作用點(或作用線),故力為向量。
2. 力的單位(SI制):絕對單位為牛頓[N],重力單位為公斤重[kgw],1 kgw 9.8 N(有時為方便計算,1 kgw≒10 N)。
二、力的作用與種類
1. 力可以使物體的運動狀態改變,或是使物體發生形變。
2. 力的種類包括了接觸力與超距力,接觸力是指兩物體間因相互接觸而產生的作用力,包括張力、彈簧力、摩擦力等;超距力則是指兩物體間不需相互接觸便可產生的力,包括重力、萬有引力、靜電力等。
三、受力分析的方法
1. 找出受力的對象。
2. 畫出力圖:根據力的來源分析受力情況,並畫出力圖。(先畫超距力,再畫接觸力)
3. 注意在作力的分析時,必須配合物體的運動狀態來加以分析處理。
四、力的合成與分解
1. 作圖法︰
- 兩力合成︰利用平行四邊形法或三角形法取向量合
- 多力合成︰利用箭頭頭尾相接的方式將多力連接,則第一個力的箭尾指向最後一個力的箭頭,即為合力
2. 直角坐標系分解法與合成法︰
- 依照題意定出相互垂直的 x 軸方向與 y 軸方向
- 將力圖上各力分解為 x 軸方向的分力與 y 軸方向的分力,再利用各方向的合力搭配計算解題
五、力平衡條件
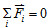 ;若為三力平衡的情況,則此三力可構成一封閉三角形,且三力必為共平面共點力(否則會有力矩產生,即非靜力平衡的狀態),並滿足拉密定理(正弦定理)︰ 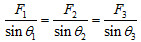 , 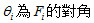 為 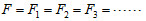 的對角。 從虎克定律到力矩
一、彈簧的串聯、並聯
1. 虎克定律︰ F=kx ,彈性體在彈性限度內,形變量與所受外力成正比,其中 F 為彈簧所受外力,k 稱為彈力常數,x 則為彈簧的形變量。
2. 串聯、並聯︰
|
串聯 |
並聯 |
| 彈力 |
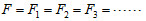 |
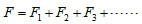 |
| 形變量 |
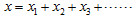 |
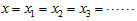 |
| 等效彈力常數 |
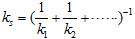
彈力常數變小 |
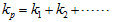
彈力常數變大 |
| 補充 |
將一彈簧分成等長的 n 段,則每一小段彈簧的彈力常數增為 nk。 |
|
二、張力
當物體受到拉力時,物體內部產生某種程度的緊繃狀態,而此一狀態會分布於物體內的各部分,各部分間達成平衡的作用力便是張力。同一繩子若質量不計,則張力在繩子各處的大小皆相等,與繩子的形狀無關。
三、力矩的計算
1. 定義:一力 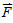 作用於剛體上的一點 P,則此力對某定點(轉點) 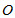 的力矩,為由 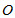 點指向 P 點的位置向量 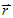 與 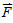 的外積。 2. 計算︰ 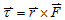 ,其中 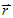 為轉軸(參考點)至剛體上某一點的位置向量, 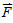 為外力; 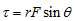 (即力矩 = 力 x 力臂),其中 θ 為位置向量與外力間的夾角。 3. 方向︰逆時針轉取正,順時針轉取負。
4. 單位︰力 x 長度,通常為 N.m 或 kgw.m。
四、力矩的效果與性質的討論
1. 計算力矩必須指定相對於哪一轉點(或轉軸),才有意義。
2. 當外力不等於零時,力矩為零的情況︰
- 力臂 r = 0 ,即通過轉點的力不產生力矩
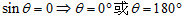 ,即力與力臂平行時不產生力矩 ,即力與力臂平行時不產生力矩 五、靜力平衡條件
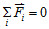 ,且 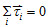 ,即合力為零,且合力矩為零(順時針的力矩等於逆時針的力矩)。 質心與重心
一、重心
一個物體(或系統)中的每一部分都受到地心引力(又稱重力)的作用,全部的重力稱為整體的重量,而整體重量的集中點就叫作重心。
對於形狀規則對稱且質量均勻分布的物體,重心為其幾何中心;對於不規則形狀的物體,可以利用懸吊法來尋找重心。
公式︰ 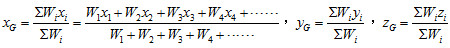 二、質心
物體(系統)的總質量集中點。
公式︰ 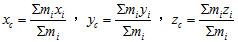 三、重心與質心的比較
1. 重心或質心的位置均不一定位於物體上。
2. 重心或質心的位置均與原點的選擇無關。
3. 在均勻的重力場中(如地球表面),重心與質心的位置相同。
4. 若無重力場作用,物體便無重心,但質心仍然存在。
牛頓運動定律
一、牛頓第一運動定律
1. 一切物質皆有保持其原有運動狀態的特性,稱為慣性;而質量愈大的物體,其慣性也愈大,慣性的大小與物體的運動速度無關。
2. 牛頓第一運動定律又稱為慣性定律,若物體不受外力作用,則靜者恆靜,動者恆作等速直線運動;無法利用實驗證明。
二、牛頓第二運動定律
1. 質量為 m 的物體,受到外力 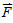 的作用時,會在外力 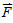 的方向上產生一加速度 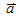 ,且其運動遵守運動方程式︰ 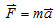 。單位︰通常使用的外力 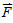 之單位為牛頓 [N],質量 m 之單位為公斤 [kg],加速度 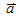 之單位為 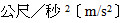 。
三、牛頓運動第二定律的解題步驟
1. 確認對象︰確認所分析的對象為單一物體或一整體系統。
2. 分析運動的起始狀態︰找出物體的初速與起點,並掌握其軌跡路線。
3. 畫出力圖︰根據力的來源畫出力圖,注意只畫外力而不畫內力。
4. 選取坐標與力的分解︰依照題意定出相互垂直的 x 軸方向與 y 軸方向,進行各力的分解(利用運動的獨立性分析各方向的運動情況)。
5. 列方程式求解︰
- 若在某方向加速度
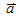 = 0,則合力 = 0,則合力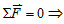 該方向列平衡方程式 該方向列平衡方程式
- 若在某方向
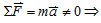 該方向列運動方程式(依據牛頓第二運定動定律列式) 該方向列運動方程式(依據牛頓第二運定動定律列式)
四、連體運動的特性與解題步驟
1. 連體運動中,各物體運動的速率均相同,即 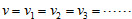 。 2. 連體運動中,各物體運動的加速度量值均相同,即 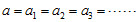 。 3. 解題步驟︰
- 先利用整體法求出整體加速度 a:
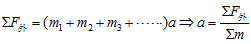
- 再利用隔離法求出各力,如系統中單一物體所受張力等
五、牛頓第三運動定律
1. 兩物體間有力的作用時,必同時產生作用力與反作用力,且兩者大小相等、方向相反,而作用於不同的物體上。
2. 作用力與反作用力的特性︰
- 必定同時產生,且作用在同一直線上
- 同時有施力體與受力體,但兩物體不一定相互接觸
- 對單獨的物體而言,作用力與反作用力屬於外力,故無法相互抵消;但對於包含兩物體的系統而言,作用力與反作用力屬於內力,故可以抵消,即無法使整個系統產生加速度
靜摩擦力與動摩擦力
一、摩擦力的產生
1. 兩物體的接觸面不光滑(摩擦係數≠0)。
2. 兩物體的接觸面相互擠壓(正向力≠0)。
3. 兩物體間企圖產生相對滑動(產生靜摩擦力),或已產生相對滑動(產生動摩擦力)時,阻止兩物體產生相對滑動的力。
二、摩擦力的性質
1. 摩擦力的方向與兩物體接觸面的切線方向平行,與兩物體間的正向力垂直。
2. 摩擦力不一定為阻力,如車輪欲前進便需依賴摩擦力的作用。
3. 摩擦力滿足牛頓第三運動定律,即 A 物體對 B 物體的摩擦力,必等於 B 物體對 A 物體的摩擦力。
三、摩擦力的種類與介紹
1. 靜摩擦力 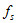 :反運動趨勢的方向, 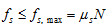 其中 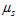 稱為靜摩擦係數,N 為正向力; 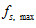 稱為最大靜摩擦力,當外力超過最大靜摩擦力時,物體便會開始移動。 2. 動摩擦力 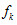 ︰反運動方向, 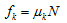 其中 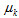 稱為動摩擦係數,N 為正向力。 3. 一般而言, 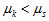 ,而摩擦係數與接觸面材料的性質、溫度有關,而與接觸面的面積無關。

|




