free hit counter
測評網[高一上][數學][第二次段考]複習錦囊
top
高一上
數學

重點回顧

一分鐘準備段考

  • 基本定義和題型要「熟」，不是只要「會」
  • 解出一題難題，勝過解十題簡單的題目，不要逃避不會的題目
  • 多做題目，培養對題型的解題感覺
  • 利用名師學院系列產品，反覆觀看、補強弱點

函數關係

一、認識函數的定義

1. 一對多不是函數關係，多對一是函數關係。
2. 若函數由集合 A 中元素對應到 B 中元素，則 A 稱為定義域， B 稱為對應域。
3. 集合 A 對應到集合 B，共可找出種不同的函數對應關係。
4. 設 f 為定義域 A 對應到對應域 B 的一個函數。 B 中被 A 的元素所對應到的元素所形成之集合，稱為值域，以表示。

斜率

一、關於斜率與範例

1. 平面上一直線 L（L 為非鉛直線），在L 上任取二點，則直線L 的斜率。（若L 為鉛直線, 則斜率不存在）
2. ax + by + c = 0 的斜率︰
  • 直線 ax + by + c = 0 的斜率為；直線 y = px + q 的斜率為 p
  • 兩直線斜率相同，則兩線重合或平行
3. 在時（即的算術平均數）有最小值。

函數性質

1. 若 f(-x) = -f(x)，則稱 f(x) 為奇函數；若 f(-x) = f(x),則稱 f(x) 為偶函數。
2. n 次單項函數圖圖形之基本特性︰
  • a＞0 且 n 為偶數

  • a＜0 且 n 為偶數

  • a＞0 且 n 為奇數

  • a＜0 且 n 為奇數
3. 平移︰
  • y = f(x-a) 的圖形為 y = f(x) 沿 x 軸正向移動 a 單位︰
  • y = f(x) + k 的圖形為 y = f(x) 沿 y 軸正向移動 k 單位︰
4. 多項式函數的係數性質︰
  • 常數項︰
  • 係數和︰
  • 偶次項係數和︰
  • 奇次項係數和︰

各種函數定理與運用

1. 恆等定理︰
  • 設 f(x)、g(x) 為不超過 n 次的多項式, 若有 (n+1) 以上個相異 x 值, 使得 f(x) = g(x)，則 f(x) 與 g(x) 為恆等式，即兩式的對應係數相等

  • 設 f(x) 為不超過 n 次的多項式，若有 (n+1) 以上個相異 x 值，使得 f(x) = k，則 f(x) 恆等於 k，即 f(x) = k
2. 除法原理︰若 f(x)、g(x) 為實係數多項式，且 g(x) ≠ 0，則必存在唯一的一組實係數多項式 Q(x) 和 R(x)，使 f(x)=g(x)xQ(x) + R(x) 成立，其中 deg R(x) ＜deg g(x) 或 R(x) = 0。
3. 餘式定理︰若 f(x) 表一多項式，則 f(x) 除以 x - a 的餘式為 f(a) 。
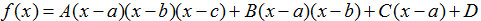
4. 牛頓插值法：設 deg f(x) = 3，已知四點函數值 f(a)、f(b)、f(c)、f(d)，則可令，再將 a 、 b 、 c 、 d 逐一代入 f(x)，可依序求出 D 、 C 、 B 、 A ，即可解出 f(x)。
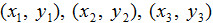
5. 拉格朗日插值法：設為坐標平面上三點，則欲尋求一多項式圖形通過此三點，可設該多項式 f(x) 為︰
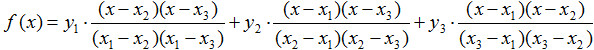
6. 韋達定理（根與係數關係）︰
7. 牛頓定理（一次因式檢驗法）︰即整係數多項式
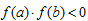
8. 勘根定理： 為實係數多項方程式, 若 （即 f(a)、f(b) 異號）, 則在區間 (a, b) 內至少存在一實根。

共軛複數

1. 共軛複數的運算︰
  • 運算後的共軛複數 = 先取共軛再運算
2. 虛根共軛定理︰為實係數方程式, 若有一根，即,則必有一根。
3. 無理根共軛定理： 為有理係數方程式, 若 f(x)=0 有一根,其中，則必有另一根。

二次函數

1. 二次函數 ：