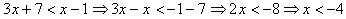1. 函數意義

(1) 意義
函數是兩組變量的對應關係。設 x、y 是兩組變量，若對於每個 x 值，必有一個且僅有一個 y 值與之對應，則這種對應關係稱為 y 是 x 函數。以 y = f (x) 表之，其中 x 為自變數，y 為應變數，而 f (x) 讀作 “f of x”，g (x) 讀作 “g of x”。
例：一輛汽車以每小時 50 公里的速度行駛，行走 x 小時，共走了 y 公里，則 x、 y 之間的關係式為 y = f (x) = 50x。將 x、y 的值列出：

x （時間）	0	1	5	...
y （距離）	0	50	250	...

(2) 函數的判斷
函數中，自變數 x 與應變數 y 可以是 1 對 1 或多對 1 的關係，但對應關係若為 1 對多或 1 對無，則不是函數關係。
例：平年當中，月分用 x 表示，天數用 y 來表示，則 x、y 的關係為 1 對 1 或多對 1，故月分 (x) 與天數 (y) 為函數關係（y 為 x 的函數）

2. 函數值的求法

將 x 用數字或文字符號代入 y = f (x) 中所得的結果，稱為函數值。
將 x = a 代入 y = f (x) 所得的值以 y = f (a) 表示，並稱 f (a) 為 y = f (x) 在 x = a時的函數值。
例：若
　　則，，
　　

1. 函數圖形

在坐標平面上，將滿足函數關係的所有數對看成坐標平面上的點坐標，並將每個數對標記在坐標平面上，再連接所有的點，所得到的圖形就是函數圖形。

(1) 線型（性）函數包含常數函數與一次函數

常數函數 在函數 y = ax + b 中，若 a = 0，則此函數稱為常態函數。 例：則即 當時，則 皆滿足則
一次函數 在函數 y = ax + b 中，若 a ≠ 0，則此函數稱為一次函數，其圖形為斜直線 例： 滿足此函數的任意兩組數對即可繪製出此圖

(2) 二次函數

在 x、y 的函數關係當中，自變數 x 的最高次方數為 2，則此函數稱為二次函數。 例： 滿足此條件的數對有 將點描繪在坐標平面上，如右圖，此類函數圖形稱為 拋物線

2. 一次函數與二元一次方程式圖形

任意一個二元一次方程式，皆可將它看成一次函數。 例： x 0 1 2 3 4 5 y 10 8 6 4 2 0

1. 不等號的意義

(1) 符號
數學符號中，「」與「」都稱為不等號。

表示法	讀法	範例	意義
	a 大於 b		大於、超過
	a 大於或等於 b	，	不小於、以上、至少
	a 小於 b		小於、未滿、不足
	a 小於或等於 b	，	不大於、不超過、以下、至多
	a 不等於 b		不相等

(2) 習慣用語

符號	用語
	大於、超過
	大於或等於、不小於、以上、至少
	小於、未滿、不足
	小於或等於、不大於、不超過、以下、至多

(3) 性質

• 遞移律：且（且）。
  　　　　且（且）。

• 若且，則

(3) 不等式
含有不等號的式子，稱為不等式。
例：，，

2. 不等式的解

若將一個數代入不等式的文字符號中，可使得不等式成立，則此數就稱為此不等式的解。
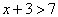
例：試問 4、5 、6 何者為不等式 的解？
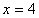
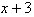
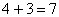
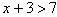
解：將代入得　∴ 4 不是的解
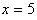
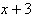
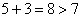
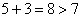
　　將代入得　∴ 5 是的解
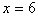
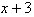
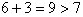
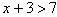
　　將代入得　∴ 6 是的解

1. 運算規則

在不等式的兩邊

(1) 同時加或減一數，不等式的符號不改變。
若，則；
例：

(2) 同時乘或除以一正數，不等式的符號不改變。
若、則；
例：；

(3) 同時乘或除以一負數，不等式的符號要改變。
　 （即變，變，變，變）
若、則；
例：；

(4) 若、，則。
例：，

(5) 若、，則。
注意：若，，則未必
　　　例：、
　　　　　但 、

(6) 若，則。
例：
若，則。
例：

2. 圖示法

在數線上表示不等式的解時，若包含該數，則該坐標點以實心點標示；若不包含該數，則該坐標點以空心點標示，如下：

(1) 若，在數線上的表示法為

(2) 若，在數線上的表示法為

(3) 若，在數線上的表示法為

(4) 若，在數線上的表示法為

(5) 若，在數線上的表示法為

(6) 若，在數線上的表示法為

(7) 若或，在數線上的表示法為

3. 一元一次不等式

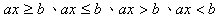
(1) 只包含一個未知數且最高次方數為一次的不等式，稱為一元一次不等式。經化簡後可得下列形式： ， 其中 x 為未知數， a 、 b 為已知常數且。

(2) 利用不等式運算規則解一元一次不等式。
例：

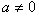
4. 絕對值不等式

設，則：

(1) 若或
　 例：或

(2) 若
　 例：