將 m 依 a ： b 的比例分成兩部分，則此兩部分分別為與。

若比例式 x ： y = a ： b ，則：

1. 比值相等，即。

2. 外項乘積 = 內項乘積，即 bx = ay。

例： x ： y = 3 ： 2 2x = 3y

3. mx ： ny = ma ： nb ，其中 m 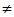0，n 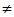0。

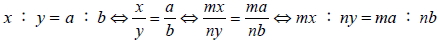
例：若 x ： y = 3 ： 2 ，則 5x ： 4y = ( 3 × 5 )：( 2 × 4 ) = 15 ： 8

4. 比例假設法
若 x ： y = a ： b ，則可設 x = ar、y = br，其中 r 0。
例：若 x ： y = 3 ： 2 ，則可假設 x = 3r 、y = 2r，其中 r 0

1. 連比例式的擴分與約分

2. 連比的求法

• 按照 x ： y ： z 的位置將兩個比排在相關位置。
• 若相同項的兩數相同，可直接寫出連比；若相同項的兩數不同，則將兩個比化成相同項的最小公倍數，再寫出連比。

例：設 x ： y = 7：4 ， y ： z = 5 ： 9，求 x ： y ： z = ?

解：
注意：將共同項化為相同的數。

將 m 依 a ： b ： c 的比例分成三部分，則此三部分分別為

1. 若 x ： y ：z = a ： b ： c，，則 x ： a = y ：b = z ： c

例： x ： y ： z = 2 ： 3 ： 4 x ： 2 = y ： 3 = z ：4

2. 比例假設法
若 x ： y ： z = a ： b ： c，則可設 x = ar、y = br 、z = cr ，其中 r 0
例： x ： y ： z = 2 ： 3 ： 4，則可設 x = 2r 、y = 3r 、z = 4r，其中 r 0

3. 若 x ： y ： z = a ： b ： c ，則 x ： my ： nz = a： mb ： nc。
例：x ： y ： z = 2 ： 3 ： 4 ，則 5x ： 3y ： 2z = ( 5 × 2 ) ：( 3 × 3 ) ：( 2 × 4 )
　　　　　　　　　　　　　　　　　　　　 = 10 ： 9 ： 8

4. 若 ax ： by ： cz = ： m ： n ，則 x ： y ： z =
例： 5x ： 3y ： 2z = 10 ： 9 ： 8 ，則 x ： y ： z = = 2 ： 3 ： 4

5. 若 ax = by = cz ，則 x ： y ： z =
例：5x = 3y = 2z = r ( r 0) x ： y ： z =

【題型一】 連比例式中若有 xy 、 yz 、 xz ，則同乘或同除以 xyz ，以化簡式子。

例 1

例 2

【題型二】 若( x + y ) ： ( y + z ) ： ( z + x) = a ： b ： c ，則假設 x + y = ar
y + z = br、 z + x = cr，其中 r 0，再將三式相加。

例 ( x + y ) ： ( y + z ) ： ( z + x) = 1 ： 2 ： 3 ，求 x 、 y 、 z 之值。
解

1. 意義： x 、y 兩個變量之間，當 y 值隨著 x 值改變，而且 y 值固定為 x 值的 k 倍（ k 為定值，k 0），則稱 y 與 x 成正比，其關係式為 y = kx。

例：數量與總價之間成正比的關係

數量 (x)	2	3	4	5	6	...	10
總價 (y)	12	18	24	30	36	...	60

若上表的數量以 x 表示，總價以 y 來表示，則 x、y 的關係式為 y = 6x

2. 性質：設 x 、y 成正比，若任意兩個 x 值的比為 a ： b ，則其對應的 y 值比也是 a ： b 。
例：承上例，若 x 的值為2、4，比為2 ： 4 = 1 ： 2，則其對應的 y 值為12、24，其比亦為 12 ： 24 = 1 ： 2

3. 常見的正比關係

• 距離 = 速率 × 時間，其中距離與速率、時間成正比。
• 三角形面積 = × 底 × 高，其中三角形面積與底、高成正比。

1. 意義：x 、y 兩個變量之間，當 y 值隨著 x 值改變，而且 x 與 y 的乘積永遠是一個定值k （ k 為定值，k 0），則稱 y 與 x 成反比，其關係式為 xy = k 。

例：兩地距離24 公里，速率（公里／小時）與時間（小時）之間成反比的關係：

速率 (x)	1	2	3	4	5	8	...
時間 (y)	24	12	8	6	4.8	3	...

若速率以 x 表示，時間以 y 來表示，則 x、y 的關係式為 xy = 24

2. 性質：設 x 、y 成反比，若任意兩個 x 值的比為 a ： b ，則其對應的 y 值比是= b ： a ；但是，若注意三個 x 值的比為 a ： b ： c ，則其對應的 y 值比 c ： b ： a。

3. 常見的反比關係

• 三角形面積 = × 底 × 高，其中底與高成反比。
• 總價 = 單價 × 數量，其中單價與數量成反比。