1. 平方根的意義
2. 符號
3. 性質
1. 原理
1. 若a、b均為正數,則︰
1. 意義︰將帶有根號的分母化為整數(有理數)的過程,稱為有理化。
2. 方法
1. 定理︰在任意的直角三角形中,「斜邊的平方等於兩股的平方和」稱為勾股定理,又稱為畢氏定理或商高定理,即
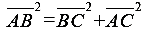
1. 使用時機︰多項式各項表面上無公因式,但將其分成若干組後,組與組之間有共同因式時。
2. 使用時機︰
2. 使用時機︰
3. 常見的完全平方試係數︰
(1, 2, 1)、(1, 4, 4)、(1, 6, 9)、(1, 8, 16)、(1, 10, 25)、(1, 12, 36)




