|
一分鐘準備段考
- 清楚定義,能自己推導公式
- 動手做題目,然後修正錯誤
- 多做題目,培養對題型的解題感覺
- 利用名師學院系列產品,反覆觀看、補強弱點
|
倍數的判別法
一、倍數的判別法
1. 「2、4、8」的倍數判別法︰
- 2 的倍數︰個位數字是偶數
- 4 的倍數︰末(尾)二位數能被 4 整除的整數
- 8 的倍數︰末(尾)三位數能被 8 整除的整數
2. 「3、9、5、11」的倍數判別法︰
- 3 的倍數︰各個位數的和是 3 的倍數
- 9 的倍數︰各個位數的和是 9 的倍數
- 5 的倍數︰個位數為 5 或 0 的整數
- 11 的倍數︰「奇數位數字和」與「偶數位數字和」的差是 11 的倍數(包含 0 )。
標準分解式
一、質數與合數
1. 質數的定義︰大於 1 的自然數中,只有 1 和自己兩個正因數的數,稱為質數。
2. 合數的定義︰大於 1 的自然數中,至少有 3 個正因數的整數,稱為合數。
3. 在1∼100中,共有︰2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97,總計25個質數。
二、質因數
1. 質因數的定義︰某整數的因數中,也是質數者。
2. 質因數的特性︰
- 任意一質數均只有 2 個正因數
- 任意一質數只有 1 個質因數
三、正因數個數與和
正整數 N 的標準分解式︰ 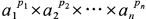
- N 的質因數有
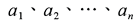 ,共 n 個 ,共 n 個
- N 的正因數個數
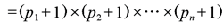
- N 的正因數總和
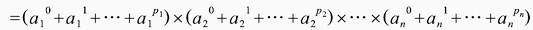
例︰已知 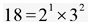 ,求其質因數個數、正因數個數與正因數總和為何?
解︰18 的質因數有 2、3,共 2 個
18 的正因數個數 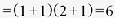
18 的正因數總和
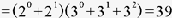
公因數與最大公因數
一、短除法︰短除法求最大公因數:提出所有公因數,再相乘。
例︰ 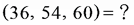 解
解︰
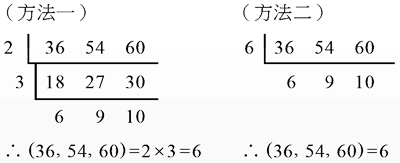
二、視察法︰
1. 以視察法求最大公因數︰
- 寫出各個整數的標準分解式
- 質因數有出現共同的才列入,且次方選小的
例︰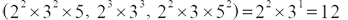
口訣︰質因數選共同的,次方選小的
公倍數與最小公倍數
一、公倍數與最小公倍數
1. 最小公倍數︰公倍數中最小的數,稱為這幾個整數的最小公倍數,符號以中括號 [ ] 表示。
2. 短除法範例︰
二、視察法
1. 視察法求最小公倍數︰
- 寫出各個整數的標準分解式
- 質因數有出現的要通通列入,且次方選大的
例︰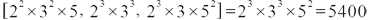
口訣︰質因數選有出現的,次方選大的
3. 最大公因數與最小公倍數之關係
餘數問題
一、除數
被除數 ÷ 除數 = 商數 … 餘數
⇔ 被除數 = 除數 × 商 + 餘數
⇔ 被除數 - 餘數 = 除數 × 商
例︰ 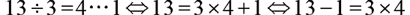
二、求除數
被除數 - 餘數 = 除數 × 商根據上述等式可知:
- 「被除數 - 餘數」或「被除數 + 不足數」為「除數」與「商」的倍數
- 「除數」與「商」為「被除數 - 餘數」或「被除數 + 不足數」的因數
- 求「除數」時,須先找出「公因數」
註︰求出「餘數」之後,記得檢查「除數」是否大於「餘數」
三、求被除數
1. 同餘數⇒被除數=公倍數+餘數
例︰a ÷ 3 = 商數 … 2 且 a ÷ 5 = 商數 … 2 (均餘2)
⇒最小被除數 a = [3, 5] + 2 = 15 + 2 = 17
2. 同不足數⇒被除數=公倍數-不足數
例︰a ÷ 3 = 商數 … 2 且 a ÷ 5 = 商數 … 4 (均不足1)
⇒最小被除數a=[3, 5]-1=15-1=14

|




