
|
單
元
回
顧
|
|

|
一分鐘準備段考
- 清楚每個物理名詞的定義
- 公式不要死記,要能推導
- 整理比較,如聲波和光波的特徵、介質中的傳遞速度等
- 利用名師學院系列產品,反覆觀看、補強弱點
|

直線運動
1. 位移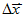 (與運動路徑無關): (與運動路徑無關):
- 定義:位置的變化量,為一向量,方向為起點指向終點
- 公式:

2. 路程S
- 定義:物體實際所經路線的總長度
- 性質:
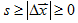 (等號成立的條件:方向不變的直線運動)
(等號成立的條件:方向不變的直線運動)
3. 平均速度(速率)
- 定義:每單位時間內的位移(路程)變化
※ x-t 圖的割線斜率為平均速度
- 公式:平均速度
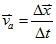 (等加速運動時: (等加速運動時: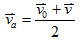 ) )
平均速率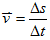
4. 瞬時速度(速率)
- 定義:極短時間內的位移(路程)變化,或質點在某一時刻的速度(速率)。
※ x-t 圖的切線斜率為瞬時速度
- 公式:瞬時速度
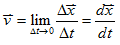
瞬時速率
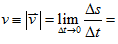 瞬時速度的量值 瞬時速度的量值
5. 平均加速度
- 定義:每單位時間內的速度變化
※ v-t 圖的割線斜率為平均加速度
- 公式:
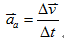
6. 瞬時加速度
- 定義:極短時間內的速度變化
※ v-t 圖的切線斜率為瞬時加速度
- 公式:

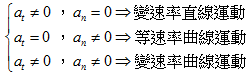
7. 加速度與速度間的關係:
- 加速度與速度同向:速度變快
- 加速度與速度反向:速度變慢
8. 等速運動:x-t 圖形為斜直線,v-t 圖形為水平直線。
等加速運動:x-t 圖形為拋物線,v-t 圖形為斜直線;a-t
圖形為水平直線。
9. 函數圖形變換原則:
10. 等加速度直線運動三大公式
11. 等加速運動的五大性質
- 等加速運動的軌跡不是直線,就是拋物線
- 時間中點的瞬時速度 = 平均速度
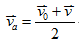
- 位移中點的瞬時速率 = 方均根速率:
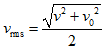
- 加速度

- 若
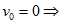 由靜止起的等加速直線運動 由靜止起的等加速直線運動
12. 自由落體:初速
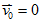 ,加速度 ,加速度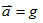 ↓的等加速直線運動。 ↓的等加速直線運動。

13. 鉛直上拋(下拋):初速為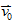 ↑(↓),加速度為 ↑(↓),加速度為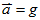 ↓的等加速直線運動。
↓的等加速直線運動。
鉛直上拋至最高點的速度為零,上升時間 =下降時間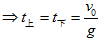 ,
,
所以飛行時間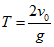 ,可達的最大高度
,可達的最大高度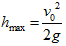 。
。
- 速度公式:上拋
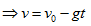 ,下拋 ,下拋
- 位移公式:上拋
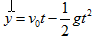 ,下拋 ,下拋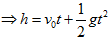
- 速度平方公式:上拋
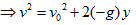 ,下拋 ,下拋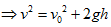
14. 光滑斜面上的加速度
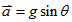 (沿斜面向下):往上滑:等減速運動;往下滑:等加速運動。 (沿斜面向下):往上滑:等減速運動;往下滑:等加速運動。
15. 相對運動:運動的描述是相對的,不同觀察者面對同一運動物體可以有不同的描述。
- 參考坐標:參考點 = 原點 = 觀察者
- 相對運動公式:
相對位置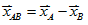 、 相對位移
、 相對位移
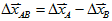 、 、
相對速度
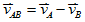 、相對加速度 、相對加速度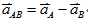

平面運動
1. 純量:只有量值而無方向的物理量。
2. 向量:同時具有量值及方向的物理量,常以 a 或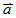 表示之。 表示之。
- 向量的解析:將一向量放入某一坐標系中,並將其分別垂直投影至各坐標軸上,配合各坐標軸的單位向量,即可在此坐標系中描述此向量。如:在
xy 平面,
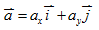 , ,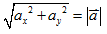
- 兩向量的加減法:
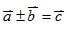 , ,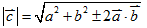 ,其中 ,其中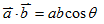 ,θ為 ,θ為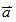 、 、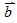 的夾角
的夾角
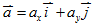 , ,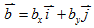 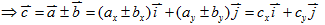
- 獨立性:互相垂直的向量可以獨立運算而不互相影響
3. 水平拋射的運動分析:
-
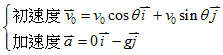
上式中θ為速度對 x 軸的夾角
- 水平位移:
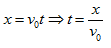 ,鉛直位移:
,鉛直位移: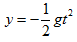 ,
,
軌跡方程式: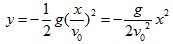 ,為拋物線軌跡, ,為拋物線軌跡,
若落下高度為 h,則物體飛行時間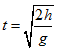 ,末速
,末速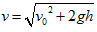
4. 切線加速度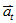 與法線加速度
與法線加速度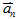 : :
-
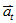 又稱加速率,改變物體運動快慢而不改變其運動方向 又稱加速率,改變物體運動快慢而不改變其運動方向
方向:平行某瞬時速度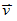 (同向加速、反向減速) (同向加速、反向減速)
-
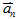 又稱向心加速度 又稱向心加速度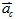 ,改變物體運動方向而不改變運動快慢 ,改變物體運動方向而不改變運動快慢
方向:垂直某瞬時速度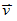 (指向軌跡的曲率中心)。 (指向軌跡的曲率中心)。
- 物體瞬時加速度
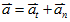 , ,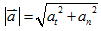
-
5. 斜向拋射:設拋射仰角為θ,則︰
- 鉛直方向:鉛直上拋運動,位移
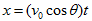
- 水平方向:等速度運動,位移
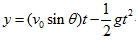
- 軌跡方程式:
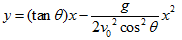 ,為拋物線軌跡 ,為拋物線軌跡
- 最大高度:
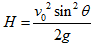 ,飛行時間: ,飛行時間: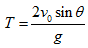
- 水平射程:
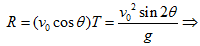 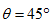 ,R有最大值
,R有最大值

6. 等速圓周運動:
- 角速度ω:單位時間內所掃過的角度
公式:ω[弧度/秒 rad/s]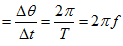
- 週期 T:每繞一圈所經過的時間。
公式:T[秒 = s]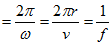 ,v 為圓周某點切線速度 ,v 為圓周某點切線速度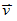 的量值 的量值
- 頻率 f:每單位時間所繞的圈數,又稱轉速
公式:f[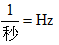 ] ]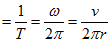 ,v 為圓周某點切線速度 ,v 為圓周某點切線速度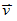 的量值 的量值
- 向心加速度
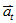 (垂直於
(垂直於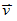 ): ):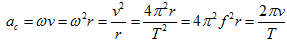
- 等速圓周運動 = 等角速度圓周運動,只有向心加速度,沒有切線加速度


|