
|
單
元
回
顧
|
|

一分鐘準備段考
- 基本定義和題型要「熟」,不是只要「會」
- 解出一題難題,勝過解十題簡單的題目,不要逃避不會的題目
- 多做題目,培養對題型的解題感覺
- 利用名師學院系列產品,反覆觀看、補強弱點
|

重點提醒
|
⊙
|
實數的運算: 結合律、交換律、分配律、消去律
|
|
⊙
|
實數的次序性質: 三一律、遞移律、加法律、乘法律
|
|
⊙
|
乘法公式: 平方公式、立方公式、平方差公式
|
|
⊙
|
有理化因式
|

有理數與無理數
1. 實數中,可表示為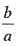 (即分數)的數,稱為有理數;不可表示為 (即分數)的數,稱為有理數;不可表示為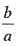 的數,稱為無理數。(其中a、b 的數,稱為無理數。(其中a、b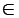 Z,a≠0) Z,a≠0)
2. 有理數系對於“+”、“-”、“×”、“÷”具有封閉性。
3. 若 a、b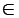 Q,a≠b,則a、b之間至少有一個有理數,稱為有理數的稠密性。 Q,a≠b,則a、b之間至少有一個有理數,稱為有理數的稠密性。
4. a、b、c、d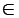 Q,若 Q,若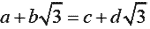 ,則有理部、無理部各別相等,即 a=c,b=d。 ,則有理部、無理部各別相等,即 a=c,b=d。

關於實數
1. 實數的運算性質:
- 結合律:(a+b)+c=a+(b+c),(ab)c=a(bc)
- 交換律:a+b=b+a,ab=ba
- 分配律:a(b+c)=ab+ac
- 消去律:若 a+b=b+c,則 a=c;若 ac=bc,則 a=b(c≠0)
2. 實數的次序性質:
- 三一律:a<b,a=b,a>b 三者有一者會成立
- 遞移律:若 a<b 且 b<c,則a<c
- 加法律:若 a<b,則 a+c<b+c
- 乘法律:若 a<b 且 c>0,則 ac<bc;若 a<b 且 c<0,則 ac>bc
3. 實數的正定性:
- 若 a
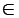 R,則 R,則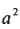 ≧0 ≧0
- 若 a、b
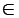 R,則 R,則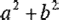 ≧0 ≧0
- 若 a、b
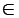 R, R,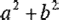 =0,則
a=b=0 =0,則
a=b=0
- 若 a、b
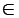 R, R,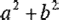 ≦0,則 ≦0,則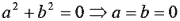

因式分解
1.
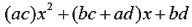 可以因式分解為 可以因式分解為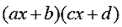 。 。
2. 有理化因式:
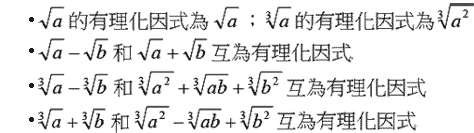

數線概論
1. 已知 A(a)、B(b) 為一數線上相異兩點則:
-
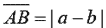
- 若 A 點在 B 點的右方,即 a>b,
則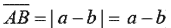
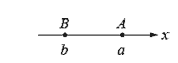
- 若 A 點在 B 點的左方,即 a<b,
則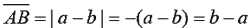
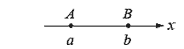
2. 數線上三點 A(a)、C(x)、B(b),已知 C 在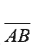 上,且 上,且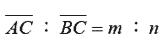 ,則 ,則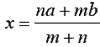
3.
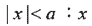 代表的點與原點的距離<a 代表的點與原點的距離<a
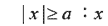 代表的點與原點的距離≧a 代表的點與原點的距離≧a


|