
|
單
元
回
顧
|
|
一分鐘準備段考
- 清楚定義,能自己推導公式
- 動手做題目,然後修正錯誤
- 多做題目,培養對題型的解題感覺
- 利用名師學院系列產品,反覆觀看、補強弱點
|

重點提醒
|
⊙
|
了解乘法交換律、乘法分配律及所推導出的十字交乘法,並確實運用在數字及文字符號的運算上。
|
|
⊙
|
認識常見的乘法公式並靈活運用在相關的問題中。
|
|
⊙
|
認識多項式及多項式的項、次數與係數,並學習多項式的排列與計算方法。
|
|
⊙
|
利用橫式、直式及分離係數等方法做多項式的四則運算,並學會多項式乘積的係數問題。
|
|
⊙
|
深入討論被除式、除式、商式及餘式之間的關係,以及多項式經四則運算後的次數問題。
|

乘法公式
1. 乘法交換律︰ab=ba
2. 乘法分配律︰
3. 十字交乘︰
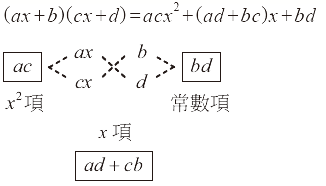
4. 和的平方公式
- 代數觀點
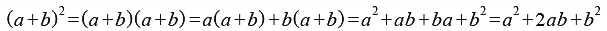
- 幾何觀點
如下圖,大正方形面積=四個矩形面積總和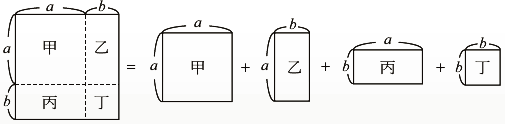
即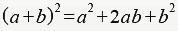
5. 差的平方公式
- 代數觀點
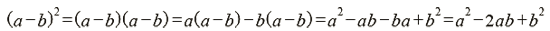
- 幾何觀點
如下圖,正方形(甲)面積=大正方形面積-兩個矩形面積+小正方形面積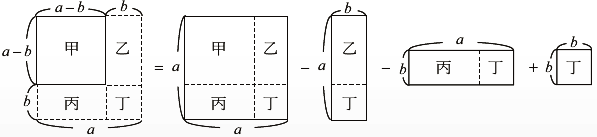
即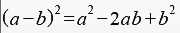
6. 三項和的平方公式
- 代數觀點
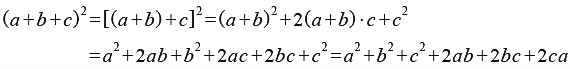
- 幾何觀點
如下圖,大正方形面積=九個矩形面積總和
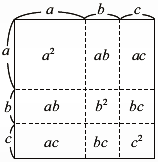
即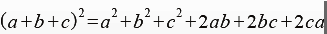
7. 求值問題常用公式

多項式
1. 多項式
- 定義:由數字和文字符號進行加法和乘法運算所構成的式子,稱為多項式
- 項:多項式中以加號分隔的每一部分連同前面的符號稱為項
- 次數:多項式中,各項文字符號的指數中為最大者,即為此多項式的次數
- 係數:多項式中,每一項文字符號前的數字稱為此項的係數
2. 多項式的判斷︰多項式中的文字符號不可在(1) 分母;(2) 根號內;(3) 絕對值內。
例如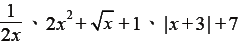 皆非多項式 皆非多項式
3. 常數多項式︰即沒有文字符號的多項式,可分為︰
- 零次多項式:只有非零的常數項
- 零多項式:0(只有常數項且常數為零,不定義其次數)

多項式的乘法
1. 十字交乘法
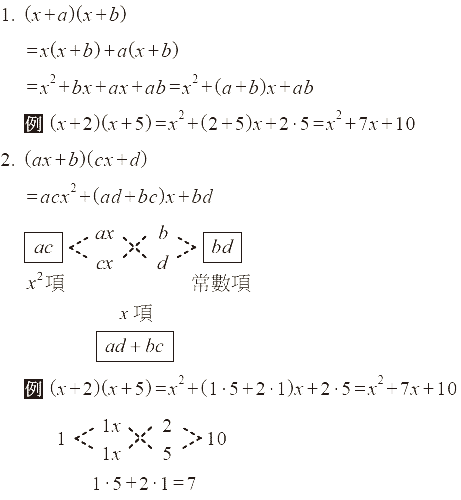
2. 多項式乘積的係數問題
若f(x)=A×B,則:
- f(x)的n次項係數為相乘後次數是n次的各組係數乘積和
例︰
- f(x)的係數總和=f(1)

多項式的除法
1. 分離係數法
例︰
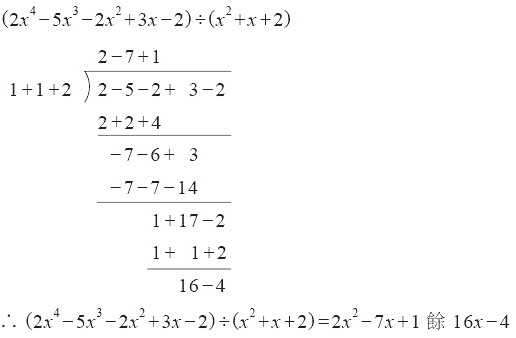
2. 除法性質︰設 A, B為多項式,
若
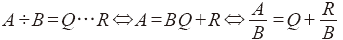 ,k為常數。 ,k為常數。


|