
|
單
元
回
顧
|
- 正數與負數
- 數線
- 相反數與絕對值
- 整數的加減法
- 整數的乘除法與四則運算
- 指數律
- 科學記號
|
一分鐘準備段考
- 清楚定義,能自己推導公式
- 動手做題目,然後修正錯誤
- 多做題目,培養對題型的解題感覺
- 利用名師學院系列產品,反覆觀看、補強弱點
|

重點提醒
|
⊙
|
負數的意義與記法。
|
|
⊙
|
數線的意義、畫法與坐標。
|
|
⊙
|
數的大小與在數線上的位置。
|
|
⊙
|
相反數與絕對值的意義。
|
|
⊙
|
正、負數的加減乘除運算。
|
|
⊙
|
整數的四則運算與規則。
|
|
⊙
|
學習指數律的記法與規則運算。
|
|
⊙
|
當底數是負數時,次方比較大小。
|
|
⊙
|
了解命數系統。
|
|
⊙
|
學習科學記號的使用,並計算科學記號的加減乘除四則運算。
|

正數與負數
1. 正、負數的意義: 在日常生活語言裡有很多相反的字,如:上與下、賺與賠、左與右、勝與負。常用符號「+」與「–」來區別,稱為性質符號。
2. 正數:大於 0 的數,叫做正數。
- 1、2、3、4、…,叫做正整數,又稱為自然數
-
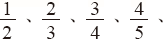 …,叫做正分數 …,叫做正分數
- 0.16、0.38、1.47、…,叫做正小數
3. 負數︰凡是小於 0 的數,叫做負數。
- -1、-2、-3、…,叫做負整數
-
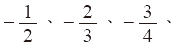 …,叫做負分數 …,叫做負分數
- -0.1、-2.36、-3.47、…,叫做負小數
4. 零
-

- 0 既不是正整數,也不是負整數,故稱為中性數

數線
1. 意義︰一直線上,用數字來表示點的位置,這個數字稱為點的坐標,此直線就稱為數線。
2. 數線的三要素
- 原點︰數線上的基準點,用 0 表示,記為 O 點
- 方向︰一般而言,原點的右方為正向,並在數線的右端畫上箭頭;反之,原點的左方為負向
- 單位長︰數線上以適當的長來表示 1 的長度,稱為單位長
3. 中點坐標︰數線上兩點 A(a)、B(b),則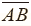 之中點M的坐標為 之中點M的坐標為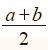 。 。

相反數與絕對值
1. 定義︰在數線上,位於原點的左右兩側,且與原點距離相等的兩點所代表的數互為相反數。
2. 相反數的延伸︰設 a 為任意數,則 a 與 -a 互為相反數。
- 正數的相反數為負數,負數的相反數為正數
- 0 的相反數為 0
- 數線上,對稱於原點的兩數互為相反數
3. 絕對值的大小
- 若a、b、c為正數,則 a>b>c ⇔ |a|>|b|>|c|
- 若a、b、c為負數,則 a>b>c ⇔ |a|<|b|<|c|
- 絕對值最小的數為 0,即 |a|≧0(a為任意數)
4. 絕對值的性質
- |x|﹦a⇒

- 當 a≥0 時,則 |a|﹦a
- 當 a<0 時,則 |a|﹦-a
- 當 a≥b 時,則 |a-b|﹦a-b
- 當 a<b 時,則 |a-b|﹦b-a
- |x|﹦|-x|
- |a-b|﹦|b-a|
- |a| + |b|﹦0⇔a﹦0且b﹦0

整數的加減法
1. 符號法則
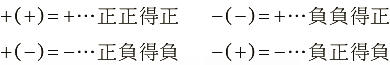
2. 當「–」連續出現︰
- 奇數個「–」 ⇒ 其結果為「–」
- 偶數個「–」 ⇒ 其結果為「+」
整數的乘除法與四則運算
1.乘法運算規則
- (+a)×(+b)=+(a×b)
- (+a)×(-b)=-(a×b)
- (-a)×(+b)=-(a×b)
- (-a)×(-b)=+(a×b)
2.乘法的性質
- 乘法交換律:甲×乙=乙×甲
- 乘法結合律:甲×乙×丙=(甲×乙)×丙=甲×(乙×丙)
3.除法運算規則
- (+a)÷(+b)=+(a÷b)
- (+a)÷(-b)=-(a÷b)
- (-a)÷(+b)=-(a÷b)
- (-a)÷(-b)=+(a÷b)
口訣
偶數個負數相乘(除)⇒結果為正數
奇數個負數相乘(除)⇒結果為負數
4. 四則運算的重要規則︰
- 有括號時,依小括號、中括號、大括號順序計算
- 先乘除、後加減
- 由左而右運算
5. 分配律
若a、b、c為任意數,則:
- a×(b+c)=a×b+a×c
- (b+c)×a=b×a+c×a
- a×(b-c)=a×b-a×c
- (b-c)×a=b×a-c×a
6. 去括號法則
若 a、b、c 為任意數,則:
- a+(b+c)=a+b+c
- a+(b-c)=a+b-c
- a-(b+c)=a-b-c
- a-(b-c)=a-b+c
7.數線上的距離與中點
假設數線上有兩點A(a)、B(b),則:
- A(a)、B(b)的距離
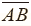 = |a-b| = |a-b|
- A(a)、B(b)的中點M的坐標為
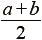

指數律
1. 指數的記法︰若a≠0,a×a×a×a=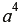 ,其中 a 為底數,4 為指數,讀作「a
的四次方」。 ,其中 a 為底數,4 為指數,讀作「a
的四次方」。
口訣
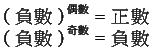
2. 指數律的規則︰已知 a、b 是不為 0 的數,且 m、n 為正整數,則:
-
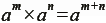 (底數相同時,兩數相乘,指數相加) (底數相同時,兩數相乘,指數相加)
-
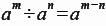 (底數相同時,兩數相除,指數相減) (底數相同時,兩數相除,指數相減)
-
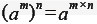 (指數為次數關係時,指數相乘) (指數為次數關係時,指數相乘)
3.
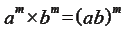
4.
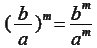
5.
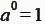
6.
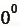 無意義 無意義
7. 次方比大小︰當底數為負數時,先比較正數大小,再比較負數大小。而當底數為正數時,可分兩種情況來討論︰
- 指數相同,底數不同
若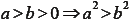
- 底數相同,指數不同
a. 若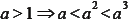
b. 若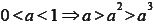

科學記號
1. 科學記號︰ 利用指數記法,將一個數寫成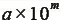 ,其中
1≤a<10,即 a 是採用小數記錄的,m 是整數;像這樣的記數方式,我們稱之為「科學記號」。 ,其中
1≤a<10,即 a 是採用小數記錄的,m 是整數;像這樣的記數方式,我們稱之為「科學記號」。
2. 科學記號的計算
3. 位數的計算
- 若將甲表示成科學記號
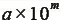 (其中 m>0),則甲有
m+1 位數。 (其中 m>0),則甲有
m+1 位數。
- 若將乙表示成科學記號
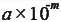 (其中 m>0),則乙的小數點後第
m 位開始不為 0 (其中 m>0),則乙的小數點後第
m 位開始不為 0


|